
\[ \]
\[ \]
\[ \]
Issue No 13, 12 December 2022
By: Anthony O. Ives
The atmosphere has a very important impact on how aircraft perform and hence on how aircraft are designed. The problem with the atmosphere is it changes from day to day as well as seasonal variations. International Standard Atmosphere (ISA) is a typical average atmosphere that you would expect in a moderate climates such as in western europe and parts of north america refered to as ISA conditions. In reality exact ISA conditions are very rarely experienced even in climates where ISA conditions are expected. So ISA conditions are generally used as a baseline and can be adjusted and compensated for depending on the variation from ISA conditions in day to day flight operations.
ISA conditions assume a sea level pressure of 101325 Pascals and a temperature of 15 degrees celsius. Degree celsius is related to degrees kelvin by adding 273.15 which would give a sea level temperature of 288.15 degrees kelvin. Sea level is considered to a pressure attitude of 0 feet. ISA conditions then assume pressure and temperature varies with altitude according to the following formulae:
\[ \frac{T}{T_0} = 1-\frac{h}{44.331} \]
\[\frac{P}{P_0} = \left( \frac{T}{T_0} \right) ^{5.256} \]
T is the temperature in kelvin, P is the pressure in pascals and the values with a 0 subscript represent the sea level values. h is altitude which is in kilometres. These equations are for altitudes below 11 kilometres which are representive of the troposphere.
Altitudes above 11 kilometres are considered to be within the stratosphere which is a isothermal stable region in upper atmostphere. Isothermal means constant temperature in this case the temperature is constant with altitude which assumes a temperature of 56.5 degrees celsius or:
\[ \frac{T}{T_0} = 0.75187 \]
However, pressure still varies with altitude in the stratosphere as described by these equations:
\[\frac{P}{P_1} = e^{-0.15769 (h- 11)} \]
\[\frac{P_1}{P_0} = 0.2234\]
Stratosphere is generally considered to exist up to 50 kilometres after which you are entering the mesosphere. In reality most aircraft really only fly in the troposphere with commercial airliners flying in the lower regions of the stratosphere during cruise. Any aircraft flying above 10000 feet (3 kilometres) require a pressured cabin or the pilots and passengers to have some sort of oxygen supply. So most small aircraft and helicopters fly in the troposphere, so unless you are flying or building a spacecraft or some other type of specialist very high altitude aircraft you only need to consider the troposphere and possibly the stratosphere for your performance calculations. The below picture gives a description of the different layers in the atmosphere and the rough altitudes they exist:
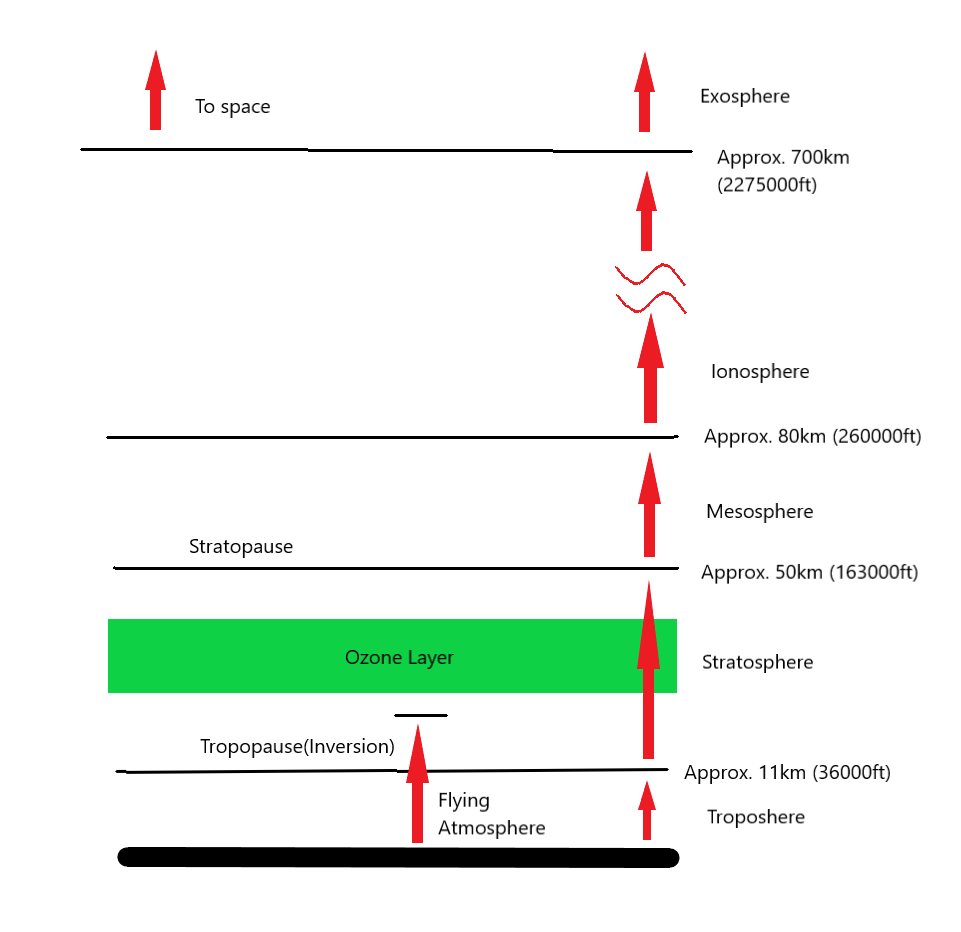
In reality the most important property of the atmosphere regarding performance is density as seen from Ref [1] and [2]. Density can be calculated using temperature, pressure and the ideal gas equation:
\[ \rho = \frac{P}{RT} \]
R is the gas constant, for dry air it is 287.052874 J Kg-1 K-1. Just as note humidity slightly reduces air density but concerning aircraft performance is rarely considered, however there are more complex forms of the ideal gas equation that take it in to consideration. Using the ideal gas equation allows you to calculate air density for non ISA conditions however there are equations similar to those for pressure using the temperature ratio calculated from altitude to give density for ISA conditions only as below:
\[\frac{\rho}{\rho_0} = \left( \frac{T}{T_0} \right) ^{4.256} \]
The above equations are for the troposphere below 11 km and the following equations for the stratosphere above 11 km:
\[ \rho_1 = P_1 \]
\[\rho_0 = 0.2971 \]
\[\rho = \rho_1 \rho_0 \]
The ISA equations are generally not used directly by engineers or pilots. The ISA equations are mostly used to create tables or programs for engineers and pilots to determine an ISA condition. Engineers are interested in all ISA properties but specifically density as it is used to calculate things like drag and lift coefficient as seen in Ref [1] and [2]. Performance charts in aircraft pilot manuals are usually referenced to temperature so pilots are typically only interested in temperature. Temperature is also easier to correct for non ISA conditions. For example the ISA sea level temperature is 15 deg C if the actual temperature is 20 deg C you can adjust the ISA temperature at altitude by +5 deg C, hence the temperature in the stratosphere would be 61.5 deg C instead of 56.5 deg C if the conditions are ISA + 5 Deg C. Hence this is how ISA conditions are corrected for day to day flight operations. Temperature variation has bigger impact on aircraft performance than pressure. Atmospheric pressure does not vary that much with the lowest sea level pressure of 950000 Pa (950 hPa or mBar) to a high of 1050000 Pa (1050 hPa or mBar) a difference of 100 hPa.
1 Pa = 1000 hPa = 1000 mBar
Pilots also use a simple more convenient way to calculate ISA conditions using lapse rate. Lapse rate is the temperature decrease with altitude for ISA it is 2 deg C per 1000 ft for the troposphere and of course it is 0 deg C per 1000 ft for the stratosphere. This way is reasonably accurate let us try using it to calculate the stratosphere temperature:
1 km = 3280.839 ft
Therefore the stratosphere is at an altitude:
11 km = 36089 ft
Therefore the temperature in the stratosphere is:
15 - (2 × 36.089) = 57.2 deg C
Very close to 56.5 deg C really of negligible different.
In the real atmosphere the lapse rate can vary at different altitudes depending on weather conditions. The lapse rate actual experienced at a present time in the atmosphere is known as the Environmental Lapse Rate (ELR). The below list gives the typical weather conditions for corresponding lapse rates:
Lapse rates greater than 3 deg C per 1000 ft mean there is instability in the atmosphere hence there is likely to be thunderstorms and heaped type clouds. 3 deg C per 1000 ft is known as the Dry Adiabatic Lapse Rate (DALR). Hence in this case ELR > DALR.
Lapse rates between 3 and 1.5 deg C per 1000 ft mean there is conditional stability in the atmosphere hence there is likely to be a mixture of weather. Hence in this case SALR < ELR < DALR
Lapse rates less than 1.5 deg C per 1000 ft mean the atmosphere is very stable with layer type clouds and a greater chance of things like fog, mist, inversions, the stratosphere is good example of a thermal inversion, but they can also occur close to ground generally as the result of radiation fog. 1.5 deg C per 1000 ft is known as the Saturated Adiabatic Lapse Rate (SALR). Hence in this case ELR < SALR.
As you can see ISA conditions assumes an average lapse of the above conditions in the troposphere where most of the atmospheric weather is, the stratosphere is generally alway stable with very little weather. The boundary between the stratosphere and troposphere is called the tropopause and is assumed to be at an altitude of 11 km (approximately 36000 ft) for ISA conditions. In reality this varies from day and day and also globally. The tropopause is lower at the poles (approximately 30000 ft or 9 km) and higher at the equator (approximately 56000 ft or 17 km) hence the altitude that the stratosphere begins and the troposphere ends changes in the same way.
Certain meteorological weather charts are published at specific pressure levels so pilots usually remember the ISA altitude associated with each particular pressure level. This is good way of remembering how pressure varies with altitude as pressure unlike temperature varies at different rates with altitude. The table gives the pressure level and corresponding ISA altitude.
| Altitude (ft) | Atmospheric Pressure (hPa) |
|---|---|
| 5000 | 850 |
| 10000 | 700 |
| 18000 | 500 |
| 30000 | 300 |
| 38000 | 200 |
| 53000 | 100 |
This article has introduced the subject of meteorology and it's importance in aviation. While I found meteorology very intetesting I cannot claim that I understood all of it but there will be future articles on the topic relevant to aviation. You can find out more about meteorology relevant to aviation and pilots in Ref [3].
Please leave a comment on my facebook page or via email and let me know how if you understand the most important atmosphere property for aircraft performance and the simplest way to calculate an ISA temperature at altitude.
References:
[1] http://www.eiteog.com/EiteogBLOG/No1EiteogBlogLiftCL.html
[2] http://www.eiteog.com/EiteogBLOG/No2EiteogBlogDragCD.html
[3] Meteorology for Pilots, Mike Wickson, 3rd Edition, 2001, Airlife Pilot's Handbooks
Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.
For any inquires contact: [email protected] copyright © Eiteog 2022